Model Predictive Path Integral (MPPI) - A Quick Introduction

Model Predictive Path Integral (MPPI) - A Quick Introduction

Model Predictive Path Integral (MPPI) Control is a powerful algorithm introduced in a 2015 publication titled “Model Predictive Path Integral Control Using Covariance Variable Importance Sampling.” Developed by a research group, MPPI offers a unique approach to controlling nonlinear systems subject to specific disturbances.

In this blog post, we will explore the core principles of MPPI, using an application case involving an RC race car navigating a sand track. As we delve into the algorithm, we’ll examine the key ideas behind MPPI, the update law that guides its optimization, and the practical implementation through an illustrative algorithm. By the end of this post, you’ll gain insights into how MPPI works and its significance in real-world applications, particularly in scenarios where precise control in the presence of disturbances is essential.

Note: This blog post is strongly based on this great video.

RC Race Car Example

To grasp the practical implications of MPPI, let’s consider a tangible example featuring an RC race car maneuvering through a sand track.

The RC race car, representing a nonlinear system, is characterized by a state defined by position and velocity. Its dynamics adhere to a partial differential equation with nonlinear terms and affine disturbances. Importantly, the system’s state is not directly observable, requiring a sensor to provide noisy measurements. These measurements, affected by process noise, serve as inputs to the MPPI controller.

The goal is to navigate the RC race car through the track, accounting for uncertainties and disturbances. The MPPI controller takes these noisy measurements, employs a cost function to evaluate trajectory desirability, and outputs control inputs. These inputs dictate the system’s evolution over time, and the process repeats iteratively.

Update Law

The update law is a mechanism that refines the control inputs based on the performance of simulated trajectories. Let’s delve into the specifics of this component:

Simulation-Based Optimization: MPPI adopts a model predictive control approach, simulating thousands of trajectories into the future. Unlike traditional methods that rely on deterministic inputs, MPPI introduces randomness. This entails applying a multitude of randomized inputs to the system model and observing their effects.

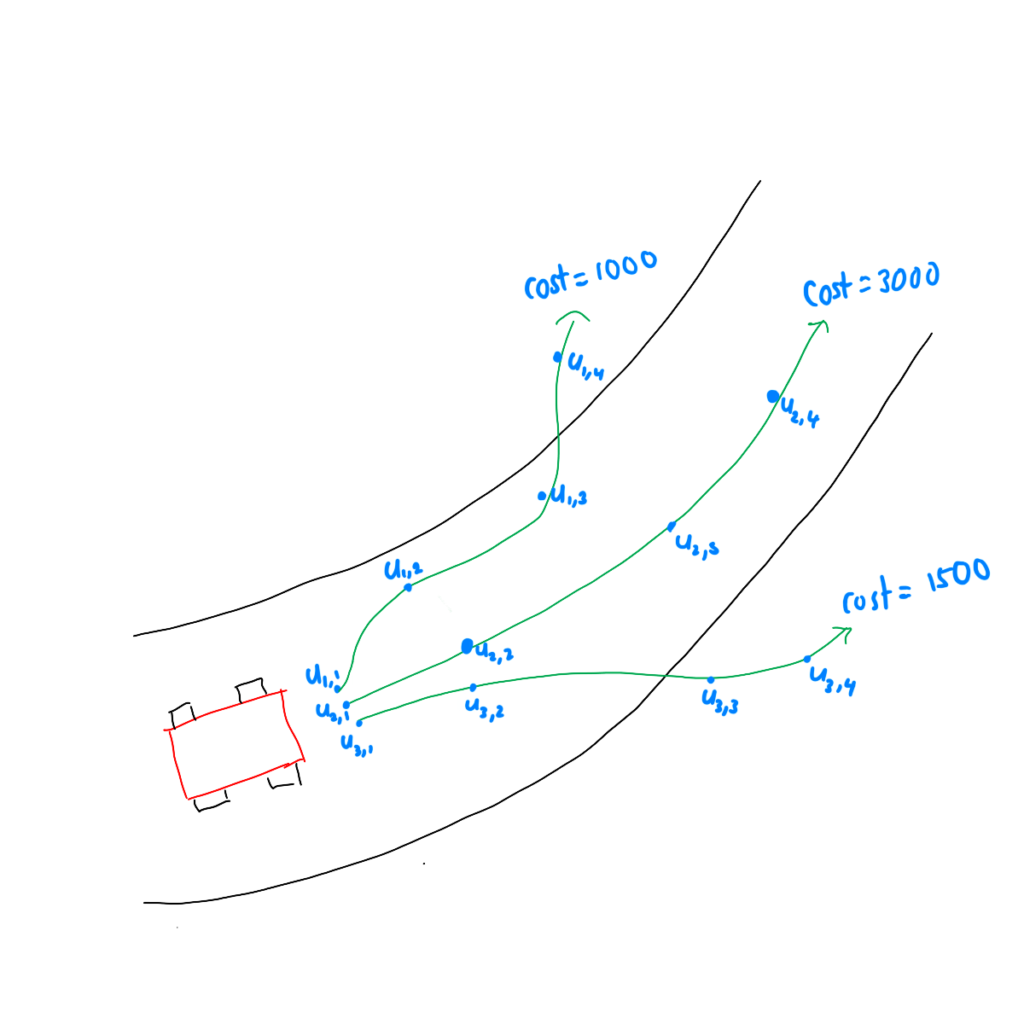MPPI trajectories MPPI Simulations

Weighted Sum for Trajectory Evaluation: The uniqueness of MPPI lies in its evaluation of the simulated trajectories. Each trajectory is associated with a cost, representing how well the system performs under the corresponding set of inputs. A weighted sum of these trajectories is computed, with weights assigned based on the quality of the resulting trajectories.

Weighted Perturbations: After simulating multiple trajectories into the future, each associated with a unique set of perturbations, MPPI calculates a weighted sum of these perturbations. The weights assigned to each perturbation are determined by the cost of the corresponding trajectory. Lower-cost trajectories receive higher weights, signifying their importance in the subsequent update. The weight assigned to a perturbation is determined by the exponential of the negative ratio of the trajectory’s cost to a constant parameter, $λ$. Mathematically, the weights ($w_k$) are calculated as below, where sk represents the cost of trajectory k.

$w_k = e^{-\frac{s_k}{λ}}$

Normalization for Coherent Update: To ensure that the weights collectively sum to one, a normalization step is applied. The sum of the weights is used to normalize the weighted perturbations, creating a coherent and balanced update that reflects the overall performance of simulated trajectories. With the weighted perturbations determined, the nominal input vector is updated using the formula:

$u = u + \frac{\sum(w_k \times \Delta u_k)}{\sum w_k}$

This update shifts the nominal inputs towards those perturbations associated with lower-cost trajectories.

As we move forward, we’ll explore how this update law translates into a practical algorithm for optimizing the RC race car’s trajectory.

MPPI Algorithm

The implementation of Model Predictive Path Integral Control (MPPI) involves a step-by-step algorithmic process, combining the core principles and the update law to optimize control inputs. The following image provides the algorithm pseudocode:

MPPI Algorithm MPPI Algorithm (source)

Let’s break down the algorithm:

  • Begin by initializing a control sequence ($u$), a vector of size N representing nominal inputs for each step ($u_0, u_1, …, u_{N-1}$). This sequence is often set to zeros initially.

  • Start an iterative loop that continues until a specified condition is met (e.g., a predetermined number of iterations).

  • In each iteration:

    • Generate random perturbations ($Δu$) corresponding to each horizon step.

    • Use these perturbations to create inputs for Monte Carlo rollouts.

      • In other words, for the kth simulation (trajectory) and $n^{th}$ perturbation ($Δu_{k, n}$), simulate how the car would move due to the perturbation using the environment model.

      • Generally, these rollouts are simulated in parallel.

    • Evaluate the total cost of each trajectory based on the simulated states.

    • Calculate weights for each trajectory based on the costs using the intuitive weighting formula.

    • Normalize the weights to ensure they sum up to one.

    • Update the nominal inputs using the weighted sum of perturbations, guided by the update law.

    • Apply the updated nominal inputs to the system.

    • Allow the system to evolve over a specified time step.

    • Observe the new state of the system.

    • Check if the termination condition is met. This could be a predefined number of iterations or a specific performance threshold.

This algorithm encapsulates the essence of MPPI, wherein the control inputs are continuously refined based on the evaluation of simulated trajectories. The utilization of randomization, the intuitive weighting mechanism, and the iterative nature of the algorithm contribute to its adaptability and effectiveness in controlling dynamic systems subject to disturbances.

Conclusion

Model Predictive Path Integral Control (MPPI) is an algorithm designed for optimizing control inputs in dynamic systems, particularly those facing uncertainties and disturbances. Through the core principles of simulation-based optimization, weighted trajectory evaluation, and an intuitive update law, MPPI adapts control inputs iteratively, leading to enhanced system performance. Illustrated through an RC race car example, MPPI’s ability to handle nonlinear dynamics and imperfect sensor measurements makes it a valuable tool for real-world applications.

Note that this blog post does not cover all the aspects of the MPPI paper. MPPI uses importance sampling instead of Monte Carlo sampling, which results in a faster convergence to the solution. Feel free to take a look at my blog post on importance sampling here or check out my other posts on AI Math here.