Transformers: A Quick Explanation with Code

Transformers: A Quick Explanation with Code

Transformers are a class of models that has gained a lot of traction over the years, especially in the domain of natural language processing and understanding.

In this post, I will discuss, part by part, how this architecture is formed. Each part will discuss a component or concept of the architecture by giving a concrete definition using code. The explanations are based on this great video by Dr. Pascal Poupart.

A few quick notes before we start

  • The only dependency for all the code sections is NumPy. This is in the hope that it’ll be clearer due to the higher transparency of NumPy.

  • Some code sections (like that of MHA), have the potential to be optimized by vectorization. However, I have chosen not to do so, to avoid complexity.

  • Due to the same reason, this post doesn’t pay much “attention” (pun unintended), to how transformers are trained, but rather focuses on how transformers can be used to generate sequences based on inputs. The prior of the two would likely require the usage of other packages such as PyTorch or Tensorflow.

Attention

Attention is essentially like a generalization of a database/dictionary.

Let’s say we have a query.

q = np.array([0, 1])

  • In a dictionary, we check if that query is equal to one of the keys, and then we get the value for that key.

  • In attention, the query doesn’t need to be equal to one of the keys. We simply look at the similarity between the query and the key, and get a sum of the values weighted by the similarities.

Regular Dictionary Method

dictionary = {
    str(np.array([0, 1])): np.array([0, 0]),    # converting to string because numpy arrays are not hashable
    str(np.array([1, 0])): np.array([1, 1])
}

print(f"Query = {q} => Value = {dictionary[str(q)]}")

# Output:
# Query = [0 1] => Value = [0 0]

Attention Method

def q_to_v(query, keys, values):
    total_sim = 0
    total_v = 0
    for i, k in enumerate(keys):
        similarity = np.dot(query, k)
        v = similarity * values[i]
        
        total_sim += similarity
        total_v += v
    
    return total_v / (total_sim or 1)


keys = np.array([[0, 1], [1, 0]])
values = np.array([[0, 0], [1, 1]])

print(f"\nQuery = {q} => Value = {q_to_v(q, keys, values)}")

# Output:
# Query = [0 1] => Value = [0. 0.]

Similarity

In the above example, we use a dot product to measure the similarity between the query and the key.

In addition to this, there are several options for measuring similarity:

  • Dot product (q.T * k)

  • Scaled dot product (q.T * k / sqrt(len(k)))

  • General dot product (q.T * W * k), where W is a trainable weight matrix

  • Additive similarity (W.T * q + W.T * k)

Multi-Head Attention (MHA) in Transformers

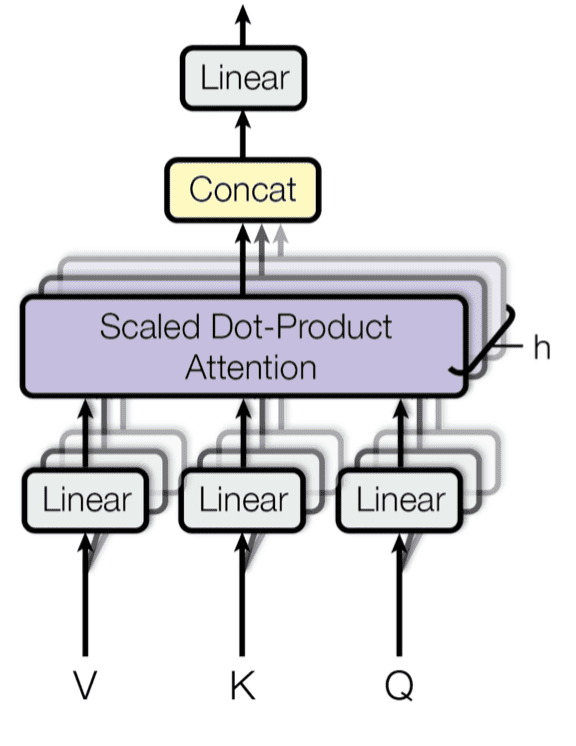Multi-head Attention architecture in Transformers Multi-head Attention architecture

As seen in the above diagram, each of the value, key, and query is first projected using 3 linear layers (you can think of it as simply multiplying by a matrix). The results of the 3 linear layers are then passed through a scaled attention mechanism.

The idea behind multi-head attention is that we can have multiple such sets that are finally concatenated and passed through a linear layer to get the output of the MHA unit. You can think of the idea behind this to be similar to kernels/filters in CNN.

The following equations can denote this entire process:

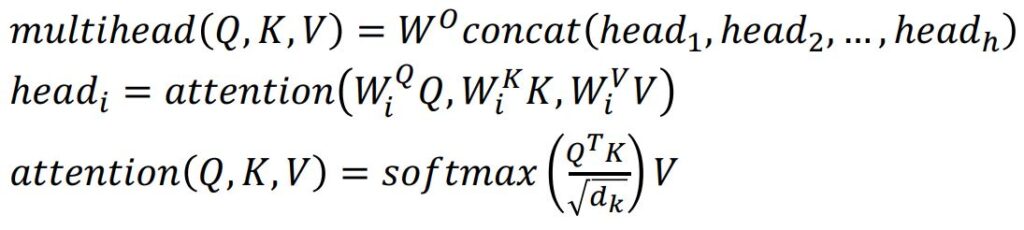MHA Equations MHA Equations

Implementation

Initialization

# Initialize queries, keys, and values
queries = np.random.random((3, 2))
keys = np.random.random((3, 2))
values = np.random.random((3, 2))

seq_len, d = queries.shape

Linear Layer

Next, I’ll define the function for the linear layer. In practice, this often gets implemented as a neural network, rather than a simple matrix multiplication. However, for the simplicity of using NumPy, I’ll treat it as matrix multiplication.

# Define the function to apply the linear layer weights onto the vector
def linear(weights, vecs):
    return (np.expand_dims(weights, 0) @ np.expand_dims(vecs, 2)).reshape(vecs.shape[0], weights.shape[0])

MHA Function

I’ll also define a function for the Multi-head Attention functionality. Here, as the inputs, q_s, k_s, and v_s refer to the queries, keys, and values, respectively. weights refer to the weights of the linear layers in the MHA module. n_heads refers to the number of heads in the MHA module.

# Define the Multi-head Attention function
def mha(q_s, k_s, v_s, weights, n_heads=4):
    W_Q, W_K, W_V, W_O = weights
    seq_len, d = q_s.shape
    
    head_outputs = []
    for i in range(n_heads):
        total_sim = 0
        total_v = 0
        
        # Linear layer
        qs_head = linear(W_Q[i], q_s)
        ks_head = linear(W_K[i], k_s)
        vs_head = linear(W_V[i], v_s)
        
        # Attention
        for i, k_head in enumerate(ks_head):
            similarity = np.exp(np.dot(qs_head, k_head) / d ** 0.5)         # (seq_len,) : one similarity for each query
            v = similarity.reshape(seq_len, 1) * vs_head[i].reshape(1, d)   # (seq_len, d) : one weighted value for each query
            
            total_sim += similarity
            total_v += v
        
        head_outputs.append(total_v / total_sim[:, None])       # broadcast and divide by total weight

    h_out = np.concatenate(head_outputs, axis=1)            # (seq_len, d * n_heads)
    
    return linear(W_O, h_out)        # (seq_len, d)

Let’s see how we can use these functions in code. I’ll first define the variables that I’ll be using.

# Number of heads
num_heads = 4

# The weight matrices
# - Initialized randomly for demonstrating
# - These, too, get tuned during training
linear_weights = [
    [np.random.random((d, d)) for _ in range(num_heads)],   # W_Q
    [np.random.random((d, d)) for _ in range(num_heads)],   # W_K
    [np.random.random((d, d)) for _ in range(num_heads)],   # W_V
    np.random.random((d, num_heads * d))                    # W_O
]

mha(queries, keys, values, linear_weights, num_heads)

Masked Multi-Head Attention in Transformers

The issue with regular MHA is that since we always input the entire sequence into the module, the module can just look up what comes next and just use that.

Masked MHA simply masks out the vectors representing the future tokens.

Implementation

def masked_mha(q_s, k_s, v_s, weights, n_heads=4):
    W_Q, W_K, W_V, W_O = weights
    seq_len, d = q_s.shape
    
    head_outputs = []
    for i in range(n_heads):
        total_sim = 0
        total_v = 0
        
        # Linear layer
        qs_head = linear(W_Q[i], q_s)
        ks_head = linear(W_K[i], k_s)
        vs_head = linear(W_V[i], v_s)
        
        # Attention
        for i, k_head in enumerate(ks_head):
            # Mask out the keys occuring in the future
            mask = np.zeros((seq_len,))
            mask[i:] = float('-inf')
            
            similarity = np.exp((np.dot(qs_head, k_head) + mask) / d ** 0.5)        # (seq_len,) : one similarity for each query for a given key
            v = similarity.reshape(seq_len, 1) * vs_head[i].reshape(1, d)           # (seq_len, d) : one weighted value for each query for a given key
            
            total_sim += similarity
            total_v += v
        
        head_outputs.append(total_v / (total_sim[:, None] + 0.0000001))       # broadcast and divide by total weight

    h_out = np.concatenate(head_outputs, axis=1)            # (seq_len, d * n_heads)
    
    return linear(W_O, h_out)        # (seq_len, d)

The usage of this function in code looks as follows:

masked_mha(queries, keys, values, linear_weights, num_heads)

Embeddings

Let’s take text as an example (although it doesn’t have to be).

Say we have a sentence: “The apple fell”

What we do is, for each word of this sentence, we find a vector that captures the meaning of the sentence. This vector is something known as an embedding vector.

The mapping from a word to its embedding vector can be achieved using a lookup table. For words, there are usually lookup tables made by other people. We can also create this lookup table by optimizing for the values of the table.

Self Attention

Self-attention simply means that the queries, keys, and values are all the same set of vectors.

The reasoning behind this is that, by passing the same set of vectors to all three inputs, we’re essentially getting a representation of how every pair of words of a sentence relates to each other.

embeddings = np.array([[0, 0], [0, 1], [0.1, 0.5]])
queries = keys = values = embeddings

Layer Normalization

It turns out that for very deep neural networks, it is difficult to perform the gradient descent updates in a smooth manner. This is because, when we update with gradient descent, we are not just updating one parameter or even one layer; we’re updating multiple layers. Since the final loss and output depend on all the layers, the target is constantly moving. Practically, normalizing the outputs of the layer has been shown to greatly improve the time and performance of gradient descent.

Generally, this means that we are simply making it so that the distribution of the outputs from a layer has mean = 0 and standard deviation = 1. However, we can also multiply the normalization expression by a scalar called the gain in order to control what the layers get normalized to.

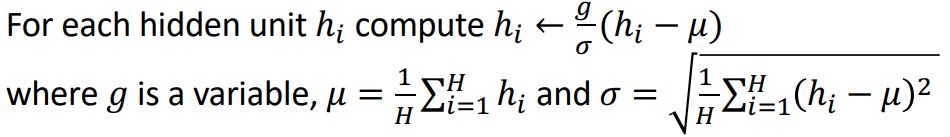Layer Normalization Layer Normalization

def layer_norm(inp, gain=1):
    return gain * (inp - inp.mean()) / inp.std()


layer_outputs = np.random.random((10,))
layer_norm(layer_outputs)

Positional Embeddings in Transformers

As you know, when it comes to getting the meaning of a sentence or text, the order of the words matters. Since we are basically getting a weighted sum of the values corresponding to different tokens of the query, by default, the order is not taken into consideration.

To address this, we can add another term to each embedding vector so that the token’s position in a sentence is also captured. This added term is known as positional embedding.

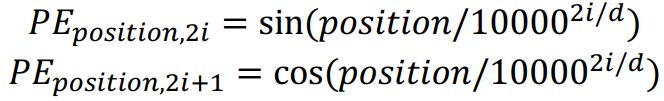Positional Embedding equations Positional Embedding equations

def get_position_encoded_embeddings(embeddings):
    seq_len, d = embeddings.shape

    pe = np.zeros(embeddings.shape)
    for pos in range(seq_len):
        for i in range(d):
            if i % 2 == 0:
                pe[pos, i] = np.sin(pos / 10000 ** (2 * i / d))
            else:
                pe[pos, i] = np.cos(pos / 10000 ** (2 * i / d))
    return embeddings + pe

Here’s an example of how we can use this function:

get_position_encoded_embeddings(queries)

Transformer

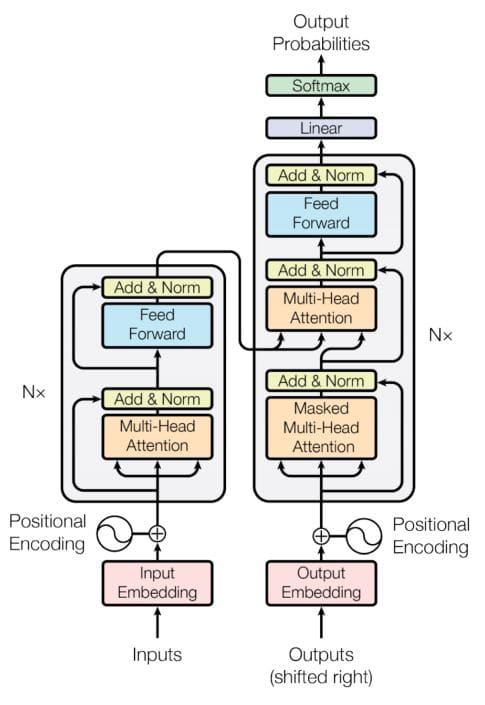Transformer Architecture Transformer Architecture

The transformer can be divided into two main components:

  • Encoder (left)

  • Decoder (right)

The inputs to both these components are summed with the positional embeddings prior to being fed into the component.

Encoder

The encoder of a transformer can be used to encode an input sentence/sequence into a vector representation.

The encoder consists of sets of blocks placed sequentially, each of which consists of the following components:

  1. Multi-head Attention Unit - Set up as self-attention

  2. Add MHA inputs to MHA outputs and apply Layer Normalization

  3. Feed Forward NN

  4. Add NN inputs to NN outputs and apply Layer Normalization

Note: The encoder, although often used, may not be a compulsory component of the architecture, based on the context. For example, a text generation task where there is no input can work without the encoder.

Decoder

The decoder of a transformer takes the encoder outputs and the previous outputs as inputs and generates a new output based on them.

The decoder, too, consists of a set of blocks, each of which consists of the following components:

  1. Masked Multi-head Attention Unit - Masks out the embeddings of the future tokens

  2. Add Masked-MHA inputs to Masked-MHA outputs and apply Layer Normalization

  3. Multi-head Attention Unit - values = keys = encoder_outputs, queries = normalized_masked_mha_outputs

  4. Add MHA inputs to MHA outputs and apply Layer Normalization

  5. Feed Forward NN

  6. Add NN inputs to NN outputs and apply Layer Normalization

Note: The decoder has two main inputs, the encoder outputs and the tokens generated up to the current state by the decoder. Since there is no such token as the first input of the decoder, the first token is usually specified to be a special start token.

Implementation

Let’s first define some variables and functions we can use in the implementation. Feel free to read the comments for an idea of what each variable defines.

def get_random_mha_weights(n_heads):
    # Generate a random set of weights for a single MHA module
    return [
        [np.random.random((d, d)) for _ in range(n_heads)],   # W_Q
        [np.random.random((d, d)) for _ in range(n_heads)],   # W_K
        [np.random.random((d, d)) for _ in range(n_heads)],   # W_V
        np.random.random((d, n_heads * d))                    # W_O
    ]


# Number of words in the vocabulary
vocab_size = 10
# Embedding length
d = 2
# Embedding definition
embedding_table = np.random.random((vocab_size, d))

# Number of heads in MHA blocks
num_heads = 4
# Number of encoder blocks
num_enc_blocks = 3
# Number of decoder blocks
num_dec_blocks = 3

# MHA linear layer weights for each MHA component
enc_mha_weights = [get_random_mha_weights(num_heads) for _ in range(num_enc_blocks)]
dec_mha_weights = [get_random_mha_weights(num_heads) for _ in range(num_dec_blocks)]

# Linear layer weights for decoder masked MHA component
dec_mmha_weights = [get_random_mha_weights(num_heads) for _ in range(num_dec_blocks)]

# Weights for linear layer after decoder
dec_lin_weights = np.random.random((d, vocab_size))


# NOTE: For the sake of keeping numpy as the only dependency and for simplicity, I will use a matrix as a substitute for the neural network.
# However, keep in mind that a neural network works somewhat differently than a linear layer since it can have multiple layers with non-linear layers between layers.
enc_nn_weights = [np.random.random((d, d)) for _ in range(num_enc_blocks)]
dec_nn_weights = [np.random.random((d, d)) for _ in range(num_dec_blocks)]

Defining the encoder and the decoder

Next, let’s define the functions of the encoder and decoder.

def encoder(enc_inputs, mha_weights, nn_weights, n_blocks=3):
    for i in range(n_blocks):
        # Self Attention with MHA + Add & Norm
        q = k = v = enc_inputs
        out = mha(q, k, v, mha_weights[i], num_heads)
        out_norm = layer_norm(out + q)
        
        # Linear + Add & Norm
        nn_out = linear(nn_weights[i], out_norm)
        nn_out_norm = layer_norm(nn_out + out_norm)
        
        enc_inputs = nn_out_norm
    
    return q

def decoder(dec_inputs, enc_outputs, mha_weights, mmha_weights, nn_weights, vocab_size, n_blocks=3):
    for i in range(n_blocks):
        # Self Attention with MHA + Add & Norm
        q = k = v = dec_inputs
        out = masked_mha(q, k, v, mmha_weights[i], num_heads)
        out_norm = layer_norm(out + q)
        
        # MHA + Add & Norm
        out_mha = mha(out_norm, enc_outputs, enc_outputs, mha_weights[i], num_heads)
        out_mha_norm = layer_norm(out_mha + out_norm)
        
        # Linear + Add & Norm
        nn_out = linear(nn_weights[i], out_mha_norm)
        nn_out_norm = layer_norm(nn_out + out_norm)
        
        dec_inputs = nn_out_norm
    
    # Take the last vector since it corresponds to the new word
    lin_out = nn_out_norm[-1] @ dec_lin_weights
    
    # Softmax
    lin_out_exp = np.exp(lin_out)
    softmax_out = lin_out_exp / np.sum(lin_out_exp)
    
    # Sample word using the probabilities from softmax
    return random.choices(range(vocab_size), weights=softmax_out)[0]

Inference

Finally, let’s use all these functions to generate a new sentence, given an input sentence.

# Input sentence
sentence = np.random.randint(0, vocab_size, size=3)
enc_embeddings = embedding_table[sentence]       # (seq_len, d)
pos_enc_embeddings = get_position_encoded_embeddings(enc_embeddings)

# Start token embedding
words = [0]
dec_embeddings = [embedding_table[0]]
pos_dec_embeddings = get_position_encoded_embeddings(np.array(dec_embeddings))

# Encoder
enc_out = encoder(pos_enc_embeddings, enc_mha_weights, enc_nn_weights, num_enc_blocks)

max_chars = 20
# Decoder loop
for _ in range(20):
    word = decoder(pos_dec_embeddings, enc_out, dec_mha_weights, dec_mmha_weights, dec_nn_weights, vocab_size, num_dec_blocks)
    if word == vocab_size - 1:
        break
    words.append(word)
    dec_embeddings.append(embedding_table[word])
    pos_dec_embeddings = get_position_encoded_embeddings(np.array(dec_embeddings))

# Output sentence
print(words)

Final Thoughts

That’s it. Hope you found it helpful.

Do keep in mind the notes/caveats I mentioned at the beginning of the post. On that note, I will try to connect these concepts with the training side of transformers, at a later date. You can keep an eye out for that here if you wish.