Monte Carlo Tree Search - A Quick Introduction (with Code)
Monte Carlo Tree Search (MCTS) is a heuristic search algorithm used in artificial intelligence and computer games for decision-making. The algorithm combines tree search with random sampling to find near-optimal solutions. It has been applied to various games such as Go, chess, and shogi and has shown promising results.
- How Monte Carlo Tree Search Works
- Upper Confidence Bound (UCB1) Score
- Advantages of Monte Carlo Tree Search
- Code Implementation
- Running MCTS
- Final Thoughts
How Monte Carlo Tree Search Works
MCTS is a probabilistic algorithm that uses random simulations to guide the search for the best move in a game. The algorithm starts with a root node representing the current game state, and iteratively
-
selects a node for expansion,
-
simulates random playouts from the expanded node, and
-
backpropagates the results to update the node statistics.
The selection of the next node is based on a balance between exploration and exploitation, where the algorithm explores promising nodes and exploits the information from the simulations.
Node
Each node consists of 3 attributes:
-
Total value (V) - The sum of rewards that were received by all episodes that had this node.
-
Visitation count (n) - The number of times this node was part of an episode.
-
State (s) - The state that the current node represents.
MCTS Process
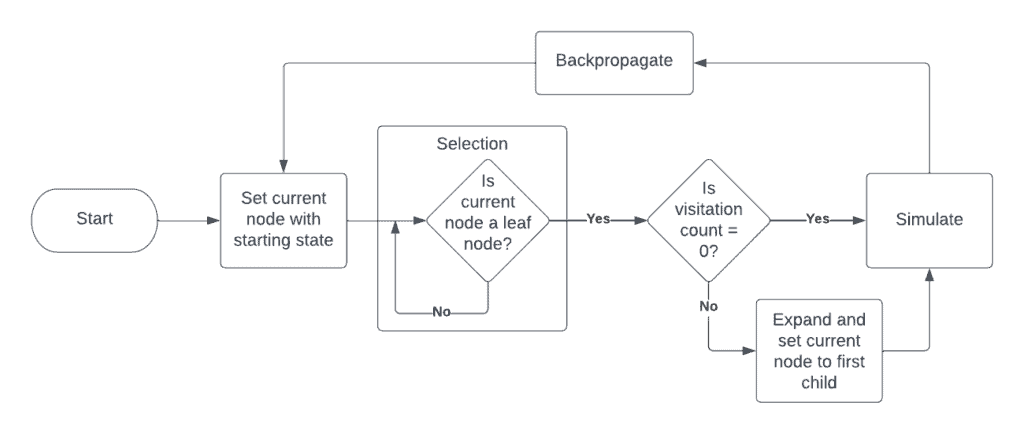
MCTS Process
MCTS works over a number of iterations. Each iteration takes place in 4 main steps:
-
Selection
-
Expansion
-
Simulation
-
Backpropagation
Note: If you’d like to see a video explanation of the process, check out this video. I found the explanation very helpful.
Selection (a.k.a. Tree Traversal)
The algorithm starts at the root node representing the current game state and selects the child node with the highest Upper Confidence Bound 1 (UCB1) score.
We’ll talk more about the UCB1 score later. But, feel free to jump over to that section if you’d like to get it clarified now.
We repeat this selection process until we reach a node that doesn’t have any children (a.k.a a leaf node).
Expansion
If we previously visited the current leaf node, then we can skip the expansion stage and go directly to the simulation stage. If not, we do the following.
From the current state, we create a new set of child nodes. Each of these child nodes represents a state that can be reached by taking an action from the current state. Therefore, the number of child nodes is equal to the number of possible actions that can be taken from the current state.
Note: The states of the child nodes don’t have to be unique if different actions can lead to the same state.
After creating nodes for the child nodes, we select one of the children (usually the first child) as our new state.
Simulation (a.k.a. Rollout)
What we want from this stage is to approximate how good the current state is. In other words, we want to find out what the best return (or reward) we can get from the current state. To do this, from the current state, we simulate until we terminate. Let’s discuss a couple of ways we can do this simulation.
-
Random actions: One of the simpler options is to choose random actions until we reach a terminal state. The issue with this is that different actions can lead to vastly different states. If this is the case, then we may not reach the best possible state from the current state (which is what we want to do)
-
Select actions using a Policy: This is the approach used by AlphaZero (the RL algorithm by DeepMind which reached the highest level in chess, go, and shogi). In short, think of the policy as a function that approximates the best action for a given state. One way to create this function is to use a neural network. AlphaZero trains a policy network using the states and actions generated by MCTS.
Backpropagation (a.k.a. Backup)
Once we have an approximation of the value of the state, we have to update all the nodes we visited along the way. Accordingly, we add the obtained return to the value of each visited state. We also add 1 to the visitation count of each state.
Upper Confidence Bound (UCB1) Score
One of the key components of Monte Carlo Tree Search (MCTS) is the balance between exploration and exploitation. MCTS does this using the UCB1 score.
Understanding the UCB1 Formula
The UCB1 formula determines the best move by calculating the average reward of each option, as well as the uncertainty of each option. The formula is defined as follows:
UCB1 = V_i + 2 \sqrt{\frac{ln N}{n_i}}
where Vi and ni refer to the value and visitation count of the current node, respectively. N refers to the visitation count of the parent node.
Let’s talk a bit about what this score means.
The Value Term
The total value of the node (Vi) is a direct part of the score. So, the higher the value is, the more the UCB1 score is.
This means that the algorithm favors nodes that have a higher value.
The Square Root Term
The numerator has the parent visitation count (N) while the denominator has the current node visitation count ni. Therefore, the higher the parent visitation count, the higher the UCB1 score. Also, the lower the current node visitation count, the higher the UCB1 score.
This means that, if a node hasn’t been visited much, it’s more likely to be picked.
We also use the natural log of the parent visitation count in the numerator. This is to manage the impact of the node visitation count. The numerator prevents the impact from being too low.
Balancing Exploration and Exploitation
The UCB1 formula balances exploration and exploitation by considering both the average reward of each option and the uncertainty of each option. During the early stages of the search, when there is a lot of uncertainty, the UCB1 formula will favor options with high uncertainty to encourage exploration. As the search progresses and more information is gathered, the average reward becomes a more important factor, and the UCB1 formula will favor options with high average rewards to encourage exploitation.
Advantages of Monte Carlo Tree Search
MCTS has several advantages compared to other tree search algorithms, such as Minimax and Alpha-Beta Pruning. Some of these advantages include:
-
Ability to handle stochastic games: MCTS can handle games with random elements, such as dice rolls or shuffled decks, by simulating the random events and estimating their impact on the outcome.
-
Handling of large search spaces: MCTS can handle large search spaces by dynamically focusing on the most promising moves, while still exploring other options.
-
No need for a priori knowledge: MCTS does not require a priori knowledge of the game, such as an evaluation function, to find near-optimal solutions.
-
Ability to incorporate learned models: MCTS can incorporate learned models, such as neural networks, to improve the accuracy of the simulations and the speed of the search.
-
Dynamic balancing of exploration and exploitation: MCTS dynamically balances exploration and exploitation through random sampling, allowing the algorithm to adapt to the game’s characteristics.
Code Implementation
Imports
Start by importing the required libraries.
import math
import copy
import random
import numpy as np
import gymnasium as gym
Here, we’re using:
-
mathfor the square root and log functions -
copyto make copies of the environment -
randomfor selecting random actions and actions according to a probability distribution -
numpyfor calculating the `softmax` of the values of each action. We use the result as a probability distribution for selecting actions. -
gymnasiumis the new version of OpenAI Gym. We use the OpenAI Gym to get the environments for our tasks.
The Node Class
Next, we define the Node class. This class holds the attributes and methods of a given node.
Attributes of the Node Class
-
value: The sum of returns that were obtained by going through this node. -
n: The number of times this node was visited. -
state: The state represented by the node. -
children: A list of the child nodes of the current node
Methods of the Node Class
-
get_child_ucb1: A method to calculate the UCB1 score of a child -
get_max_ucb1_child: A method to get the child with the max UCB1 score and its index
Implementation
# Define the node class
class Node:
def __init__(self, state=None):
self.value = 0
self.n = 0
self.state = state
self.children = []
# Method to calculate the UCB1 score of a child
def get_child_ucb1(self, child):
if child.n == 0:
return float("inf")
return child.value / child.n + 2 * math.sqrt(math.log(self.n, math.e) / child.n)
# Method to get the child with the max UCB1 score and its index
def get_max_ucb1_child(self):
if not self.children:
return None
max_i = 0
max_ucb1 = float("-inf")
for i, child in enumerate(self.children):
ucb1 = self.get_child_ucb1(child)
if ucb1 > max_ucb1:
max_ucb1 = ucb1
max_i = i
return self.children[max_i], max_i
MCTS Class
We use the MCTS class to make a decision on what action to take next. For each new state, we create a new instance of the MCTS Class.
Attributes of the MCTS Class
-
env: The copy of the environment to find be used to find the next best action -
start_env: A copy of the copy of the environment to reset to the initial state -
root_node: The root node of the search tree
Methods of the MCTS Class
-
run: Run MCTS for a specified number of iterations. -
traverse: Traverse the currently explored tree, expand if necessary, and select a node to simulate from. -
rollout: Simulate until a terminal state is reached. Here, we’re using random actions to do the simulation. -
backpropagate: Update the value and visit counts up the visited nodes of the current episode.
Implementation
class MCTS:
def __init__(self, env, reset=False):
self.env = env
if reset:
start_state, _ = self.env.reset()
else:
start_state = self.env.unwrapped.state
self.start_env = copy.deepcopy(self.env)
self.root_node = Node(start_state)
for act in range(self.env.action_space.n):
env_copy = copy.deepcopy(self.env)
new_state, _, _, _, _ = env_copy.step(act)
new_node = Node(new_state)
self.root_node.children.append(new_node)
# Run `n_iter` number of iterations
def run(self, n_iter=200):
for _ in range(n_iter):
value, node_path = self.traverse()
self.backpropagate(node_path, value)
self.env = copy.deepcopy(self.start_env)
vals = [float("-inf")] * self.env.action_space.n
for i, child in enumerate(self.root_node.children):
vals[i] = (child.value / child.n) if child.n else 0
return np.exp(vals) / sum(np.exp(vals))
def traverse(self):
cur_node = self.root_node
node_path = [cur_node]
while cur_node.children:
cur_node, idx = cur_node.get_max_ucb1_child()
self.env.step(idx)
node_path.append(cur_node)
if cur_node.n:
for act in range(self.env.action_space.n):
env_copy = copy.deepcopy(self.env)
new_state, _, _, _, _ = env_copy.step(act)
new_node = Node(new_state)
cur_node.children.append(new_node)
cur_node, idx = cur_node.get_max_ucb1_child()
self.env.step(idx)
node_path.append(cur_node)
return self.rollout(), node_path
def rollout(self) -> float:
tot_reward = 0
while True:
act = random.randrange(self.env.action_space.n)
_, reward, done, _, _ = self.env.step(act)
tot_reward += reward
if done:
break
return tot_reward
def backpropagate(self, node_path: list, last_value: float):
for node in node_path[::-1]:
node.value += last_value
node.n += 1
Running MCTS
Here, we create instances of MCTS and choose actions using them, until we reach a terminal state. For choosing each action, we run MCTS for 20 states. You can change this based on the number of actions. Increase the iteration count if there’re a lot more actions.
if __name__ == '__main__':
env = gym.make('CartPole-v1')
env.reset()
done = False
tot_reward = 0
while not done:
mcts = MCTS(copy.deepcopy(env), reset=False)
probs = mcts.run(20)
action = random.choices(range(len(probs)), weights=probs, k=1)[0]
_, reward, done, _, _ = env.step(action)
tot_reward += reward
print(f"Reward: {tot_reward} ", end='\r')
Final Thoughts
Hope you found this post helpful! MCTS is the search algorithm behind some of the most influential papers in the past few years; not just AlphaZero, but also AlphaTensor, which is being used to find fast matrix multiplication sub-operations. I might make a blog post going into detail on how these are implemented. In the meantime, feel free to head over to the reinforcement learning section of this blog to see my explanations for several other concepts in RL.